2022 | UGRACTF | CRYPTO

noteasy03

题目¶

Цезарь скривился,
Замкнулся в себе.
Преумножение.

Caesar curved, closed in on himself. Multiplication.

rzua]o^]tahf]ie]kiho^z]niru]ha^ogn]doak]i[]g[uff]iop^atpe[paz[[tapzetd

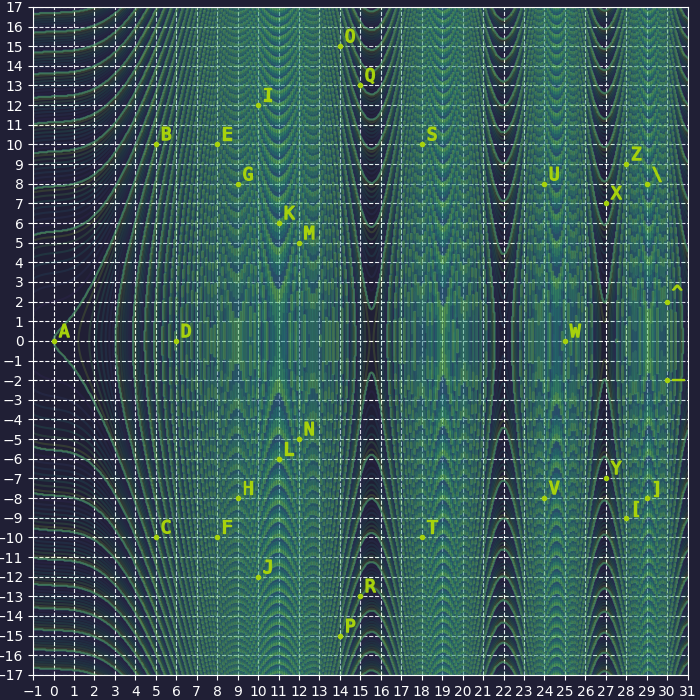
解题思路 English ver.¶

根据题目 curved/closed in on himself 和图片，推测应该是某种曲线，且所有点在曲线上都能找到对应点
分析密文，结合 flag 的格式，得到以下映射关系。再结合 Caesar 推测是单表代换
```
r -> u
z -> g
u -> r
a -> a
] -> _
```
排除常见的单表代换密码（都是线性的），最后想到了椭圆曲线
尽管点分布的形状似乎和实数域的椭圆曲线不搭边，但若考虑是在有限域，则图中点集完全符合有限域中椭圆曲线的特性
- 同时，椭圆曲线上点的逆元可以符合加解密的映射需求
根据各点坐标大小可推出有限域大小为 \(31\)
通过在线椭圆曲线可视化工具寻找椭圆曲线系数的大致范围
- 关键特征：三个点位于 \(x\) 轴，一个点位于 \((0, 0)\)

再结合有限域和已知点的坐标确定椭圆曲线系数 \(a=-5,b=0\)

from Crypto.Util.number import *

ps = [(0, 0), (5, 10), (5, 21), (6, 0), (8, 10), (8, 21), (9, 8), (9, 23), (10, 12), (10, 19), (11, 6), (11, 25), (12, 5), (12, 26), (14, 15), (14, 16), (15, 13), (15, 18), (18, 10), (18, 21), (24, 8), (24, 23), (25, 0), (27, 7), (27, 24), (28, 9), (28, 22), (29, 8), (29, 23), (30, 2), (30, 29)]

for a in range(-5, 0):
    for b in range(-4, 5):
        if 4 * a**3 + 27 * b**2:
            E = EllipticCurve(Zmod(31), [a, b])
        else: continue
        f = 1
        for p in ps:
            try: E(p[0], p[1])
            except:
                f = 0
                break
        if f: print(a, b)

根据 Caesar 和 Multiplication 推测点的映射为椭圆曲线中的点乘，系数为 \(3\)，然而解密的结果是一堆乱码 :(

最早的凯撒密码为移 \(3\) 位，后来扩展为移位密码。于是尝试改变系数，当系数为 \(11\) 时成功获得 Flag XD

from Crypto.Util.number import *

cipher = 'rzua]o^]tahf]ie]kiho^z]niru]ha^ogn]doak]i[]g[uff]iop^atpe[paz[[tapzetd'

E = EllipticCurve(Zmod(31), [-5, 0])
d = {E(0, 0): 'a', E(5, 10): 'b', E(5, 21): 'c', E(6, 0): 'd', E(8, 10): 'e', E(8, 21): 'f', E(9, 8): 'g', E(9, 23): 'h', E(10, 12): 'i', E(10, 19): 'j', E(11, 6): 'k', E(11, 25): 'l', E(12, 5): 'm', E(12, 26): 'n', E(14, 15): 'o', E(14, 16): 'p', E(15, 13): 'q', E(15, 18): 'r', E(18, 10): 's', E(18, 21): 't', E(24, 8): 'u', E(24, 23): 'v', E(25, 0): 'w', E(27, 7): 'x', E(27, 24): 'y', E(28, 9): 'z', E(28, 22): '[', E(29, 8): '\\', E(29, 23): ']', E(30, 2): '^', E(30, 29): '_'}
res = dict()

for k, v in d.items():
    res[v] = d[11 * k]

for c in cipher:
    print(res[c], end='')

Flag¶

ugra_in_case_of_losing_your_sanity_dial_oh_three_oijnacjfhjaghhcajgfcd

最后更新: 2022年4月22日 23:55:03

Contributors: YanhuiJessica

noteasy03

题目¶

解题思路 English ver.¶

Flag¶

评论