跳转至
2021 | ByteCTF | Crypto

easyxor

题目

Block cipher is used frequently.

easyxor.py 
#! /usr/bin/env python
from Crypto.Util.number import bytes_to_long, long_to_bytes
from random import randint, getrandbits


def shift(m, k, c):
    if k < 0:
        return m ^ m >> (-k) & c
    return m ^ m << k & c


def convert(m, key):
    c_list = [0x37386180af9ae39e, 0xaf754e29895ee11a, 0x85e1a429a2b7030c, 0x964c5a89f6d3ae8c]
    for t in range(4):
        m = shift(m, key[t], c_list[t])
    return m


def encrypt(m, k, iv, mode='CBC'):
    assert len(m) % 8 == 0
    num = len(m) // 8
    groups = []
    for i in range(num):
        groups.append(bytes_to_long(m[i * 8: (i + 1) * 8]))
    last = iv
    cipher = []
    if mode == 'CBC':
        for eve in groups:
            cur = eve ^ last
            cur_c = convert(cur, k)
            cipher.append(cur_c)
            last = cur_c
    elif mode == 'OFB':
        for eve in groups:
            cur_c = convert(last, k)
            cipher.append(cur_c ^ eve)
            last = cur_c
    else:
        print 'Not supported now!'
    return ''.join([hex(eve)[2:].strip('L').rjust(16, '0') for eve in cipher])


if __name__ == '__main__':
    from secret import flag
    if len(flag) % 8 != 0:
        flag += '$' * (8 - len(flag) % 8)
    length = len(flag)
    num = length // 8
    keys = [randint(-32, 32) for _ in range(4)]
    IV = getrandbits(64)
    front = flag[:length // 2]
    back = flag[length // 2:]
    cipher1 = encrypt(front, keys, IV, mode='OFB')
    cipher2 = encrypt(back, keys, IV)
    print cipher1 + cipher2

解题思路

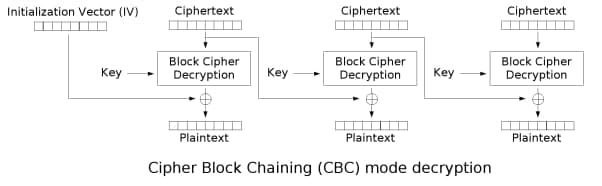
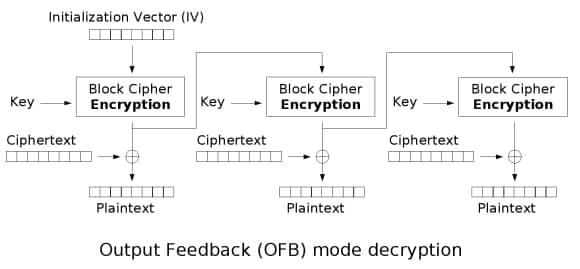
  • 涉及到两种分组密码工作模式：CBC 和 OFB

  • 无论 CBC 还是 OFB 都可以从第二组密文开始解密（由第一组密文推出第二组 IV），期间可爆破出 keys

    CBC 解密

    • CBC -> 使用第一组密文作为从第二组开始解密的 IV，由于 Block Cipher Decryption，需要编写 convert 函数的逆过程

      OFB 解密

    • OFB -> 根据 Flag 格式可知第一组明文为 ByteCTF{，与第一组密文异或得从第二组开始解密的 IV

    • 由于解密必须使用 (╥ω╥)，逆一下 convert() 函数，重点在逆 shift() 函数上
    def unconvert(m, key):
    c_list = [0x37386180af9ae39e, 0xaf754e29895ee11a, 0x85e1a429a2b7030c, 0x964c5a89f6d3ae8c]
    for t in range(3, -1, -1):
        m = unshift(m, key[t], c_list[t])
    return m

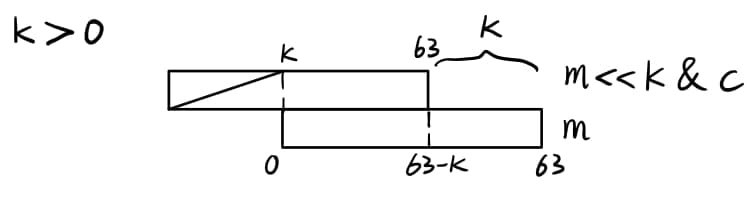
  • shift() 函数中移位导致部分位泄漏（当 \(k == 0\) 时无法逆推）

    • 当 \(k > 0\) 时，结果二进制各个位依次为 \(m_0 \oplus m_k \& c_{0}，m_1 \oplus m_{k+1} \& c_{1}，...，m_{63-k} \oplus m_{63} \& c_{63-k}，m_{64-k}，m_{65-k}，...，m_{63}\)
      推理图解

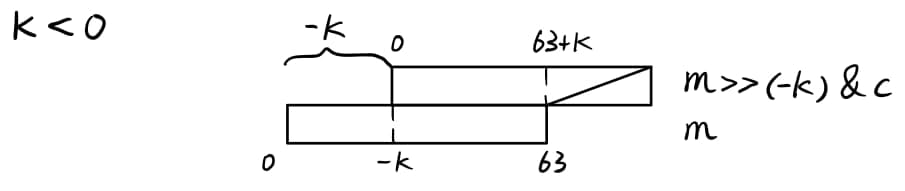
    • 当 \(k < 0\) 时，结果二进制各个位依次为 \(m_0，m_1，...，m_{-k} \oplus m_0 \& c_{-k}，m_{-k+1} \oplus m_1 \& c_{-k+1}，...，m_{63} \oplus m_{63+k} \& c_{63}\) 推理图解

    • unshift() 函数 

      def unshift(m, k, c):
    if k == 0: return 0    # 返回任意值即可
    res = m
    if k < 0:
        for _ in range(64 // (-k)): # 每一轮可以计算 k 位
            res = m ^ res >> (-k) & c
    else:
        for _ in range(64 // k):
            res = m ^ res << k & c
    assert m == shift(res, k, c)
    return res

  • 解密函数 decrypt() 改写自 encrypt() 

    def decrypt(c, k, iv, mode='CBC'):
    assert len(c) % 16 == 0
    num = len(c) // 16
    groups:list = []
    for i in range(num):
        groups.append(int(c[i * 16: (i + 1) * 16], 16))
    last:int = iv
    plain = []
    if mode == 'CBC':
        for eve in groups:
            cur = unconvert(eve, k)
            plain.append(cur ^ last)
            last = eve
    elif mode == 'OFB':
        for eve in groups:
            cur = convert(last, k)
            plain.append(cur ^ eve)
            last = cur
    return ''.join([long_to_bytes(eve).decode() for eve in plain])

  • 四重循环爆破密钥，通过 OFB 或 CBC 模式都可以，获得密钥数组：[-12, 26, -3, -31] 

    cipher = "89b8aca257ee2748f030e7f6599cbe0cbb5db25db6d3990d3b752eda9689e30fa2b03ee748e0da3c989da2bba657b912"
length = len(cipher)
cipher1 = cipher[:length // 2]
cipher2 = cipher[length // 2:]

for k1 in range(-32, 33):
    for k2 in range(-32, 33):
        for k3 in range(-32, 33):
            for k4 in range(-32, 33):
                keys = [k1, k2, k3, k4]
                try:
                    res = decrypt(cipher1[16:], keys, int(cipher1[:16], 16) ^ bytes_to_long(b"ByteCTF{"), 'OFB')
                    # res = decrypt(cipher2[16:], keys, int(cipher2[:16], 16))
                    flag = 1
                    for i in res:
                        if ord(i) not in range(32, 127):    # 过滤含不可打印字符字符串
                            flag = 0
                    if flag:
                        print(res, keys)
                except:
                    continue

  • 从而可推出 IV 并计算 Flag 

    keys = [-12, 26, -3, -31]
out = bytes_to_long(b"ByteCTF{") ^ int(cipher1[:16], 16)
iv = unconvert(out, keys)
print(decrypt(cipher1, keys, iv, 'OFB') + decrypt(cipher2, keys, iv))

# ByteCTF{5831a241s-f30980q535af-2156547475u2t}$$$

参考资料

最后更新: 2021年10月26日 11:03:26
Contributors: YanhuiJessica

评论